附录

中文马克思主义文库 -> 参考图书·左翼文化 -> 〔英〕本·法因、劳伦斯·哈里斯《重读〈资本论〉》（1979）

附录

《论《资本论〉第三卷中马克思的基本理论结构的改正问题》

〔俄〕拉迪斯·冯·鲍特凯维兹

　　最初发表在德国《国民经济和统计年鉴》（1907年7月）上。1948年由美国保尔·M·斯威齐译成英文。

　　到目前为止，马克思的评论家们还很少更严密地考察过《资本论》第三卷中关于从价值到生产价格的转化和平均利润率的决定的过程，以便看看其中是否就没有矛盾。
　　在这方面，涂干—巴莱诺斯基是一个例外^[1]。他曾明确地指出，马克思计算平均利润率的方法是不正确的。而且，他还曾指出，如何依据既定的生产价格和平均利润率正确地计算出相应的价值和剩余价值率来是可能的。假使是这样的话，那么，就提出了一个同马克思试图解决的相对立的问题。
　　然而，指出马克思是在什么方法上犯了错误，而没有颠倒他提出问题的方法，是令人感兴趣的。为此目的，为了不使表述复杂化，介绍一下涂干—巴莱诺斯基使用的同样有限制的假设是合适的，这种假设即：全部预付资本（包括不变资本）每年周转一次，重新再现在每年产品的价值或价格中^[2]。在属于论证马克思的错误这个问题的限度内，使用这种有限制的假定是完全无可非议的，因为不约束在这种特殊情况内，就不能要求一般的正确性。
　　另一方面，下面的做法同涂干—巴莱诺斯基是一致的。马克思由以构成社会生产总体的不同生产领域，可以概括为三个生产部门：部门Ⅰ生产生产手段，部门Ⅱ生产工人的消费品，部门Ⅲ生产资本家的消费品。同时假定，分别用于部门Ⅰ、Ⅱ、Ⅲ的三级生产手段生产的资本有机构成是相同的。
　　最后，假定是“简单再生产”。
　　以C₀、C、C，V₁、V₂、V和 S₁、S、S₃分别代表部门Ⅰ、部门Ⅱ、部门Ⅲ的不变资本、可变资本和剩余价值。简单再生产的条件表示为如下的方程式体系：
　　（1） C₁＋V₁＋S₁＝C₁＋C₂＋C₃
　　（2） C₂＋V₂＋S₃＝V₁＋V₂＋V₃
　　（3） C₃＋V₃＋S₃＝C₁＋S₂＋S₃
　　如果以r代表剩余价值率，则　　　　

　　于是，（1）（2）（3）式可重新写成：
　　（4） C₁＋（1＋r） V₁＝C₁＋C₂＋C₃
　　（5） C₂＋（1＋r） V₂＝V₁＋V₂＋V₃
　　（6） C₃＋（1＋r） V₃＝S₁＋S₂＋S₃
　　现在的问题是，遵照利润率相等的规律，把价值表现转换成生产价格表现。
　　马克思的解答首先存在于形成这样的总数中
　　（7） C₁＋C₂＋C₃＝C
　　（8） V₁＋V₂＋V₃＝V
　　（9） S₁＋S₂＋S₃＝S
　　其次，以p代表平均利润率，则
　　（10）

　　最后，三个部门生产的商品的生产价格表示为
　　 C₁＋V₁＋P（C₁＋V₁）
　　 C₂＋V₂＋P（C₂＋V₂）
　　 C₃＋V₃＋P（C₃＋V₃）
　　在这里，生产价格的总和等于价值的总和，或者等于总价值（C＋V＋S）。
　　问题的这种解决办法是不能同意的，因为它从转化过程中排除了不变资本和可变资本，而相等利润率的原理，当它代替马克思意义上的价值规律时，是必须包括这些因素的。^[3]
　　从价值量到价格量的正确转变，可以如下地作出：
　　假定部门Ⅰ产品的价格同价值的变动系数（平均）为x，部门Ⅱ的为y，部门Ⅲ的为z。并假定三个部门的利润率共同为p（现在公式10不再被认为是p的正确表现了）。
　　现在，同方程式（4）、（5）、（6）相对应的体系如下：
　　（11）（1＋p）（c₁x＋v₁y）＝（c₁＋c₂＋c₃）x
　　（12）（1＋p）（c₂x＋v₂y）＝（v₁＋v₂＋v₃）y
　　（13）（1＋p）（c₃x＋v₃y）＝（s₁＋s₂＋s₃）z
　　在这里，有三个方程式和四个未知数（x、y、z和p）。为了弥补缺落的第四个方程式，我们必须确定价格单位同价值单位之间的关系。
　　如果我们按照总价格等于总价值的方法选择价格单位，我们就不能不作如下安排
　　（14） C_x＋V_y＋S_z＝C＋V＋S
　　这里，
　　（15） C＝c₁＋c₂＋c₃
　　（16） V＝v₁＋v₂＋v₃
　　（17） S＝s₁＋s₂＋s₃
　　如果，另一方面，价格单位同价值单位被认为是相等的，那么我们就不能不考虑三个部门中的那一个部门的产品充作价值和价格单位。如果黄金是这样一种商品，则
　　（18） z＝1
　　于是，未知数就减少为三个（x、y和p）。
　　为了得出最简单的可能公式，让我们建立如下的表达方式：

　　并且，l＋p＝σ
　　考虑到（1）、（2）、（3），方程式（11）、（12）、（13）可以重新写成：
　　（19） σ（x＋f₁y）＝g₁x
　　（20） σ（x＋f₂y）＝g₂y
　　（21） σ（x＋f₃y）＝g₃
　　从（19），可得：
　　（22）

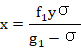
　　将其代入（20），则
　　（23）（f₁—f₂）σ²＋（f₂g₁＋g₂）^σ—g₁g₂＝0
　　由此，可得出（24）

　　或者，另外写成
　　（25）

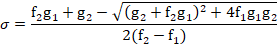
　　它容易地表示出，在这个情况下，二次方程式（23）适合于问题的条件只有一个解。如果（f₁—f₂）﹥0，则在公式（24）的平方根前加上一个负号，就可以得到σ﹤0。另一方面，如果（f₁—f₂）﹤0，则在公式（25）的平方根前加上一个正号，结果是

　　并且，更加不容置疑地是

　　这同方程式（20）相矛盾，该方程式给出

　　从方程式（20）和（21），我们发现：
　　（26）

　　并且，当我们解出σ和y时，x就能够依照公式（22）计算出来。
　　现在让我们通过几个数字的例子，来看看这些公式如何能够用于价值到价格的转化。例如，假定给出价值表现如下：

表1		价值计算
生产部门	不变资本	可变资本	剩余价值	产品价值
Ⅰ	225	90	60	375
Ⅱ	100	120	80	300
Ⅲ	50	90	60	200
总计	375	300	200	875

　　由此，我们得出以下的价值数字：
　　 c₁＝225，c₂＝100，c₃＝50，v₁＝90，v₂＝120，
　　 v₃＝90，s₁＝60，s₂＝ 80，s₃＝60，以及f₁＝²∕₅，
　　 f₂＝⁵∕₆，f₃＝⁹∕₅，g₁＝⁵∕₃，g₂＝3，g₃＝4。
　　公式（25）（26）和（22）给出：
　　 σ＝⁵∕₄，所以p＝¹∕₄，y＝¹⁶∕₁₅，x＝³²∕₂₅，我们得到：

表2		价格计算
生产部门	不变资本	可变资本	利润	产品价值
Ⅰ	288	96	96	480
Ⅱ	128	128	64	320
Ⅲ	64	96	40	200
总计	480	320	200	1000

　　在部门Ⅰ，不变资本的价格表现（288），是由相应的价值表现（25）乘以＝［³²∕₂₅］得来；可变资本的价格表现（96），是由相应的价值表现（90）乘以［¹⁶∕₁₅］得来；利润（96）是由（288＋96）乘以利润率（¹∕₄）得出。其他部门的数字，是按照相同的方法计算出来的。^[4]
　　价格总额超过价值总额产生于这个事实：其产品充作价值和价格计量尺度的部门Ⅲ的资本有机构成相对较低。但是，利润总额在数量上等于剩余价值总额的事实，是充作价值和价格计算尺度的商品属于部门Ⅲ这个事实的结果。
　　把表2中的价格与利润的关系同马克思在这种情况下所可能得到的价格与利润的关系作一个比较，是不无兴趣的。按照公式（10），马克思可能写成p＝²⁰⁰∕₆₇₅＝⁸∕₂₇，因为（依照表l）S＝200，C＝375，V＝300。
　　我们得到：

表3	按照马克思的价格计算
生产部门	不变资本	可变资本	利润	产品价值
Ⅰ	225	90	93 9/27	400 9/27
Ⅱ	100	120	65 5/27	285 5/27
Ⅲ	50	90	41 13/27	181 13/27
总计	375	300	200	875

　　这样，在不同部门产量的价格（408 9/27，285 5/27，181 13/27）和不变资本、可变资本与利润的数量表现之间就出现了不一致。象已经指出过的，马克思在这种情况下确定的平均利润率是8∕27或29.6%，而根据正确程序计算是1∕4或25%。^[5]
　　但是，马克思不仅没有表明在价值和剩余价值既定关系的基础上确定利润率的正确方法，而且他还被他的错误的价格构成理论错误地引入对确定利润率高度的诸因素的不正确的理解。他持有的主张是，在既定的剩余价值率前提下，利润率的大小取决于包括所有生产领域的社会总资本有机构成的高低。这种观点来自马克思用公式（10）来表示利润率的事实。如果我们象前面一样，指定r为剩余价值率，q₀为不变资本的价值与资本总额的比例关系，即
　　 r＝S∕V，q₀＝C∕（C+V）
　　于是我们有：
　　（27） p＝（1—q₀）r
　　依此，剩余价值率为既定，则影响利润率高度的唯一情况是，资本总额中不变资本的份额和商q₀的大小；并且，不论不同生产领域的资本有机构成有任何区别，利润率也是没有差别的。
　　诚然，在《资本论》中，我们看到决定一般利润率的有两个因素：（1）不同生产领域的资本有机构成，从而各个生产领域有不同的利润率；（2）社会总资本在这些不同生产领域的分配。但是，马克思在其计算图解中处理这两种因素时，却是让我们把它们缩减到一个单一因素，即社会总资本的有机构成。
　　让q₁代表部门Ⅰ中的不变资本同该部门资本总额之比，y₁代表部门Ⅰ的资本总额在社会总资本中的份额；同样，q₂、y₂和q₃、y₃代表部门Ⅱ和部门Ⅲ的类似的量。它们用公式表示如下：
　　 c₁∕（c₁+v₁）＝q₁，c₂∕（c₂+v₂）＝q₂，c₃∕（c₃+v₃）＝q₃；
　　（c₁+v₁）∕（C+V）＝y₁，（c₂+v₂）∕（C+V）＝y₂，（c₃+v₃）∕（C+V）＝y₃
　　从这些公式，显露出：
　　（c₁+c₂+c₃）∕（C+V）＝y₁q₁＋y₂q₂＋y₃q₃
　　并且，由于以c₁＋c₂＋c₃＝C，C∕（C+V）＝q₀，所以，
　　（28） q₀＝y₁q₁＋y₂q₂＋y₃q₃
　　现在，如果将(28)代入(27)中的q₀，并且考虑到y₁＋y₂＋y₃＝1这个事实，则得：
　　（29）p＝［y₁（1-q₁）r+y₂（1-q₂）r+y₃（1-q₃）r］∕（y₁+y₂+y₃）
　　这个公式非常清楚地表现了马克思的观点：一般利润率（p）显露为特殊利润率（1—q₁）r、（1—q₂）r和（1—q₃） r的算数平均，（1—qp）r、（1—q₂）r和（1—q₃）r在平均数的形成中分別成为y₁、y₂和y₃的“加权”。在马克思的观点中，决定一般利润率的两个因素，其一，按照公式（29），是由q₁、q₂和q₃代表的；另一个是由y₁、y₂和y₃代表的。然而，从公式（28）来看，很明显这两个因素可以缩减为一个单一因素，即由q₀代表的社会总资本的有机构成。
　　同这个观点相对立，我们可以利用一个适当的数字例子来表示：由于公式（27）和（29）是不正确的，因而这些情况是可能的，即在既定的剩余价值率前提下，一个并相同的利润率与社会总资本的不同有机构成是一致的。以下列价值图解作为一个起点：

表4	价值计算
生产部门	不变资本	可变资本	剩余价值	产品价值
Ⅰ	300	120	80	500
Ⅱ	80	96	64	240
Ⅲ	120	24	16	160
总计	500	240	160	900

　　用此表同表相比，我们发现剩余价值率是相同的（66 ²∕₃%），而资本有机构成较高。按照表1，q₀＝³⁷⁵∕₆₇₅＝0.556；而按照表4，q₀＝⁵⁰⁰∕₇₄₀＝0.676。马克思可能说，利润率必须从29.6%下降到21.6%。
　　现在，如果我们利用正确的转化方法于此表，象从表1到表2所作的那样，我们发现x＝³²∕₃₅，y＝¹⁶∕₂₁，p＝¹∕₄，完整的结果是：

表5	价格计算
生产部门	不变资本	可变资本	利润	产品价值
Ⅰ	274 2/7	91 3/7	91 3/7	457 1/7
Ⅱ	73 1/7	73 1/7	36 4/7	182 6/7
Ⅲ	109 5/7	18 3/7	32	160
总计	457 1/7	182 6/7	160	800

　　表4象表1那样有相同的利润率（25%）的理由是：按照公式（25），某种剩余价值率是既定的，利润率（p＝σ—1）完全依赖于部门Ⅰ和部门Ⅱ的资本有机构成（与此相联系，有必要记住f₁、f₂、g₁和g₂的数量的意义），以及在这方面表1和表4是完全相同的。但是，在部门Ⅲ不变资本与资本总额的比率已经从大约36%增长到大约83%的情况，同利润率的高度无关。至于其余的，从利润来源于“剩余劳动”这个利润理论的观点来看，这个结果也几乎没有什么令人惊奇的。李嘉图曾经指出过，只是触及到不进入工人阶级消费的商品的生产关系的变化，不会影响利润率的高度。^[6]
　　现在让我们考虑一下这种情况，在这里不管社会总资本有机构成仍然保持不变的事实，利润率也发生了变化。把表1和表2同下表进行一下比较，这种情况就发生了：

表6	价值计算
生产部门	不变资本	可变资本	剩余价值	产品价值
Ⅰ	205	102	68	375
Ⅱ	20	168	112	300
Ⅲ	150	30	20	200
总计	375	300	200	875

　　遵循公式（25）、（26）和（22），我们得到

　　一个完整的结果是：

表7	价格计算
生产部门	不变资本	可变资本	利润	产品价值
Ⅰ	170.3	44.1	97.1	311.5
Ⅱ	16.6	72.6	40 5	129.7
Ⅲ	124.6	13	62.4	200
总计	311.5	129.7	200	641.2

　　按照马克思的转化方法，将会再次产生相同的利润率26.6%（代替45.3%），以及总利润在三个部门中的分配会如下：部门Ⅰ 90 26/27（代替90.1），部门Ⅱ 55 19/27（代替40.5），部门Ⅲ 53 9/27（代替62.4）。
　　马克思转化方法的错误性质甚至十分明显地来自一种特殊情况，在这里部门Ⅱ没有不变资本。下表就是这种情况：

表8	价值计算
生产部门	不变资本	可变资本	剩余价值	产品价值
Ⅰ	180	90	60	330
Ⅱ	0	180	120	300
Ⅲ	150	30	20	200
总计	330	300	200	830

　　在这种情况里，为了计算p或σ的目的，我们可以不再使用公式（25），因为f₂＝∞，g₂＝∞。我们不得不转而回到方程式（11（12）、和（13）。因为c₂＝0，从（12）我们发现
　　 1＋p＝（v₁+v₂+v₃）∕v₂
　　由于公式（2），我们也可以写成（仍然由于c₂＝0）：
　　 1＋p＝（v₂+s₂）∕v₂
　　最后， p ＝s₂∕v₂
　　或者 p＝r
　　利润率等于剩余价值率，这样，根据表8，就等于2/3或66 2/3%。如果把p的价值放入公式（11）或（13），得到两个具有两个未知数（x和y）的一次方程式，因为这里z＝1，我们发现：x＝10/13，y＝2/13。价值到价格、剩余价值到利润的转变给出：

表9	价格计算
生产部门	不变资本	可变资本	利润	产品价值
Ⅰ	138 6/13	13 11/13	101 7/13	253 11/13
Ⅱ	0	27 9/13	18 6/13	46 2/13
Ⅲ	115 5/13	4 8/13	80	200
总计	253 11/13	46 2/13	200	500

　　然而，按照马克思，有关的数量关系则是如下：

表10	按照马克思的价格计算
生产部门	不变资本	可变资本	利润	产品价值
Ⅰ	180	90	85 5/7	355 5/7
Ⅱ	0	180	57 1/7	237 1/7
Ⅲ	150	30	57 1/7	237 1/7
总计	330	300	200	830

　　利润率是［200∕630］或31.8%（代替了66 2∕3%！）。
　　在这个场合，以部门Ⅱ不存在不变资本为特征，马克思推导价值和利润的不正确是特别明显的。因为很清楚，在资本家的支出只包括可变资本并且正好商品是由那个部门所生产的部门Ⅱ，不管有关的商品的价格是高或低，资本家的所得必须同他们的支出永远保持同样的比例关系。不论是通过商品交换，还是通过“价格调整”，这种比例关系从66 2∕3%减少到31.8%，是没有办法的。
　　跟随表9，我们可以表示商品交换如下：^[7]

　　可以看出，就每一组的资本家来说，购买的商品的价格总和等于销售的商品的价格总和。而表10表现出不同的情景：

　　在这里，部门Ⅰ和部门Ⅲ的资本家收进的比付出的少，而相反地，部门Ⅱ的资本家收入的相当于付出的二倍多。
　　无论如何，这个例证，在其中c₂＝0，不仅对十分清楚地表明马克思的价值到价格的转变方法引向何等的自相矛盾是有用的，而且也十分适合于充当对我们以前说明的必要补充的一个出发点。
　　有人可能倾向于从这个事实：在这个特别专门的例证中，利润率单纯地等于剩余价值率；以及从这个事实：利润率完全独立于部门Ⅰ和部门Ⅲ的资本有机构成，以至于这两个部门的有机构成可以是任何高度而不会造成利润率下降的结果，来作出结论。如果这是真实的，并且不顾它是一个特例，则几乎不可能抑制住关于用“剩余劳动”解释利润的正确性的强烈怀疑。
　　然而，事情的真实性在于，部门Ⅰ和部门Ⅲ的总投资中的不变资本的份额，如果这两个部门的利润率也等于r，就不可能超过一定限度。如果在方程式（11）中用r代替p，同时考虑到方程式（4），我们得到：
　　（1＋r）（c₁x＋v₁y）＝〔c₁＋（l＋r）v₁〕x
　　从中得出
　　　　　　 c₁r＝（1＋r）v₁x
　　以及
　　　　　　 c₁﹤［（1+r）∕r］v₁
　　另一方面，由于方程式（1），以及c₂＝0，我们有
　　　　　　 c₃＝（1＋r）v₁
　　让我们引进新的表示
　　（1＋r）²∕r＝β 和（c₁＋c₃）∕（c₁＋v₁＋c₃＋v₃）＝q′
　　现在我们得到不等式
　　（30）　　 c₁＋c₃﹤βv₁
　　所以
　　　　　　 1＋（v₁+v₃）∕（c₁+c₃）﹥1＋（v₁+v₃）∕βv₁
　　或者

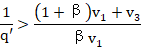
　　作为结果
　　（31）

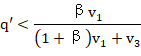
　　于是，更不容置疑地：

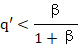
　　或者
　　（32）

　　无论如何，数量q′是部门Ⅰ和部门Ⅲ联合资本的有机构成的表现。所以，利润率之独立于部门Ⅰ和部门Ⅲ的资本有机构成，在部门Ⅱ没有不变资本的场合下，根本不意味着其他两个部门的资本有机构成可以无限制地高。事情的真实情况更确切地是，如果不变资本在这些部门中的份额，数量q′，超过了一定限度，利润率的均等化就成为不可能。
　　为了确定q₀也即不变资本在社会总资本中的份额的最高限，最恰当的是从不等式（30）出发，该不等式又可写成（c₂＝0）：
　　 C﹤βV₁
　　我们有

　　所以：
　　（33）

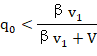
　　从这个关系式
　　（34）
　　无论如何，我们得到：
　　　　　　　　 V＝v₂＋rV₂
　　因为另一方面
　　　　　　　　 V＝v₁＋v₂＋v₃
　　它呈现出：
　　　　　　　　 v₁＋v₃＝rv₂
　　结果
　　　　　　　　 v₁﹤rv₂
　　如果我们在（33）中用rv₂代替v₁，我们就可以无容置疑地得到

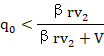
　　或者，考虑到（34），
　　（35）

　　因此，如果象我们在前面的例子中所假定的剩余价值率为66 2/3%，那么，投资于部门Ⅰ和部门Ⅲ的不变资本就决不会超过社会总资本的5/8。
　　这个例证，在其中c₂＝0，也就是说在部门Ⅱ中没有不变资本，就讲这么多。
　　同样地，如果c₁＝0，利用公式（24）或（25）来确定利润率是不可能的，因为这里f₁＝∞，g₁＝∞。如果我们把方程式（11）和（12）作为确定p和σ的基础，我们就很容易地发现：
　　（36）

　　其中的r，象以前一样，表示剩余价值率（ QUOTE ）。这个最后的方程式也可以从方程式（23）推导出来，如果用g₁去除它的系数。由于c₁＝0，

　　从r出现在（36）而不出现在（23）的事实，来假定在C₁不是零的场合，利润率独立于剩余价值率，是完全错误的。这是因为数量g₁和g₂依赖于r。我们有：
　　　　　　 g₁＝1＋（1＋r）f₁
　　和
　　　　　　 g₂＝1＋（1＋r）f₂
　　如果我们通过引入数量q₁、q₂和r，而从方程式（23）中排除了数量f₁、f₂、g₁、g₂，那么，就出现了下列的关系式：

　　由此，利润率仅仅依赖于剩余价值率（r）和投资于部门Ⅰ与部门Ⅱ的资本有机构成，就立即显而易见了。
　　如果抽象掉c₂＝0的特殊例证，利润率是永远小于剩余价值率的。这一点可以证明如下：
　　从方程式（11），我们发现
　　　　　　　　 c₁x＋v₁y﹤（c₁＋c₂＋c₃）x
　　考虑到（4），
　　　　　　　　 v₁y﹤（1＋r）v₁x
　　从此随之而来的

　　从方程式（12），出现了这个不等式：

　　或者，考虑到（9），

　　最后
　　 1＋p﹤1＋r
　　以及
　　（37）　　　　 p﹤r
　　 p的另一个最高限可以按照下列方法，从（11）中推导出来。我们有：

　　　　（1＋p）c₁x﹤（c¡＋c₂＋c₃）x

　　因此
　　（38）

　　这个不等式让我们得出结论：在一个既定的剩余价值率（r）和一个既定的可变资本的数量的前提下，没有利润率的下降，不变资本的无限制的增长不可能发生。
　　由（4）随之而来的是：
　　　　　　 c₂＋c₃＝（1＋r）v₁
　　这意味着，在部门Ⅱ和部门Ⅲ中不变资本的增长，在剩余价值率的高度和任便的可变资本总额的大小上，找到了一个限制。还应该记得V，形成V的一部分。
　　我们有同样正当的理由可以说，在部门Ⅱ和部门Ⅲ中不变资本的增长，在劳动量上找到了一个限制，劳动量是社会在任意一个既定经济时期所有的。假定这个数量为H，其中h₁属于部门Ⅰ，h₂属于部门Ⅱ，h₃属于部门Ⅲ，从而H＝h₁＋h₂＋h₃。如果我们指定劳动量等于一个价值单位如η，那么，我们有：
　　 h₁＝（v₁＋s₁）η，h₂＝（v₂＋s₂）η， h₃＝（v₃＋s₃）η
　　以及 H＝（V＋S）η
　　现在我们可以写成
　　　　　　　　　　（c₂＋c₃）η＝h₁
　　由于h是H的一部分，它显示：按照所包含的（物化）劳动量计量的投入部门Ⅱ和部门Ⅲ的不变资本，受到（活）劳动量的限制，该劳动量指在相应的经济时期可用于生产的。
　　然而，至于涉及到投入部门Ⅰ的不变资本（c₁），可以设想它在不打乱经济均衡条件的前提下会无限期地增长，如同在方程式（4）、（5）和（6）中所表现的那样。但是，象公式（38）所表示的，部门Ⅰ不变资本增长的后果迟早必然是利润率的下降。至于其他情况，不等式（38）甚至在c＝0的情况下也是有效的。
　　如果根据以上所说，与马克思相对立地认为利润率一般不依赖于社会总资本的有机构成，那将是完全不正确的。马克思用以进行理论运行的p和q₀之间的简单关系——见方程式（27）——是不存在的，并且可以构造一些实例，在其中剩余价值率（r）给定，而利润率（p）保持不变，即使q₀具有不同的价值，正象即使q₀不变而p可以采取不同的价值这种实例是可能的一样。但是——这不应该被忽略——这些实例是以三个部门资本有机构成不同的假定为基础的。如果，另一方面，q₁＝q₂＝q₃的条件实现了，那么价值和价格就是相等的，并且公式（27）就开始生效了。
　　这最后的论述不能为原谅马克思服务。因为，如果使公式（27）生效的条件实现了，那么价值转变为价格的全部运行就是无意义的，而马克思关于这种运行明确地利用了这个公式。
　　上述议论只是引向反对这种批评的。这种批评认为，不管数量q₁、q₂和q₃是否相等，马克思关于社会总资本的有机构成对利润率高度的影响的命题，就象这个命题在公式（27）中有所表现的，是不正确的。
　　涂干—巴莱诺斯基特别在这点上有错误。他试图用以反驳马克思的命题的两个数量例子，是明确地以假定所有三个部门的资本有机构成相等为特征的，换句话说就是q₁＝q₂＝q₃＝q₀。
　　在一个例子中，r（剩余价值率）从1下降到7/9，而同时q₀从2/3增加到20/29，由此出现了，完全与公式（27）一致，p（利润率）从1/3下降到7/29。^[8]
　　在另一个例子中，r从1上升到81/44，而同时q₀也从2/3增加到25/36，由此，再一次与公式（27）一致，p从1/3增加到9/16。
　　涂干—巴莱诺斯基从这个事实得出结论：在一种情况下，不变资本份额的增长伴随着利润率的下降，在另一种情况下，又伴随着利润率的上升；一般利润率是完全独立于社会资本的有机构成的；所以，马克思的利润理论是不正确的。^[9]
　　好象这些数字例子在任何方面都会触及到马克思关于社会总资本的有机构成对利润率的影响的理论！按照马克思，这种影响只是在如果剩余价值率保持不变时，才使它自身感觉到是一种预示。

^[1] 《马克思主义的理论基础》（莱比锡，1905），第170～188页。

^[2] 这个假定也可以在例如考茨基的《卡尔·马克思的经济学说》（斯图加特，1903，第98页）里找到。

^[3] 关于这一点的更进一步的考察，见我的著作《马克思体系中的价值计算和价格计算》的第二篇论文，《社会科学与社会政治文献》，第25卷，第1期（1907年7月）。

^[4] 表1是取自前面提到的涂干—巴莱诺斯基的那个著作，表2所有的数字也都是与他相应的数字有关的。涂干—巴莱诺斯基用劳动单位代替货币单位创立了他的价值图解。这是足够合理的，但它把注意力从价值计算和价格计算之间的真实区别转移了。

^[5] 见我的著作《价值计算与价格计算》的第一篇论文，《社会科学与社会政治》，第23卷第一期，第46页。

^[6] 关于这一点的更进一步的考察，见我的著作《价值计算与价格计算》中的第三篇论文。

^[7] 为了简单起见，假定资本家以实物预付消费品给他们的工人们，因而工人们不直接参与商品交换。

^[8] 对q₀我一直理解为可变资本的价值同资本总额的价值的比例关系，而在涂干—巴莱诺斯基的例中，它是一价格表现的问题。按价值，q₀＝C∕（C+V）；按价格，q₀表现为C_x∕（C_x+V_y）。但是，如果假定，象涂干—巴莱诺斯基那样，在所有三个部门的资本有机构成是一致的，则这两种表现方式是一致的。因为在这个场合，x＝y，或者x＝y＝1。

^[9] 例如，《资本论》（英文版）第三卷，第75、248页。在马克思的利润率下降规律中，这个限制条件估计到什么程度，我在我的著作《马克思体系中的价值计算和价格计算》中的第三篇论文里曾进行过详尽的讨论。